【算数脳から数学脳へ切り替えよう！】数学は未知数を表すことからはじめる

茗荷谷の個別指導塾ESCAの岸田です。数学が苦手科目であると思っている人は多いですが、その原因は様々です。大きく分けると、一つは「定義・定理、計算方法、（できれば基本解法も）」などのルールが覚えられていないということ、もう一つは「未知数を表せていないこと」が挙げられます。
※もうひとつ「体系化できていない」ということが挙げられますが、これは上記の二つが身についてからです。
さて、算数と数学の違いはなんでしょう、という問いに、多くの方が文字を使うか、使わないかということを挙げられますが、感覚的にはそれも間違ってはいないのかなと思います。算数的な思考で数学の問題を考えたときに、非常に解き難いことが多いのですが、その理由の一つが、数学には文字によって複数の変量を表すことができるという強みがあるからです。では、その文字をどのように使いこなせば良いのかを、本記事では記していきたいと思います。
＜目次＞

• 1.未知数を文字でおこう
  


• 2.他のものを表してみよう


• 3.表した量の関係式を考えてみよう


• 4.まとめ

1．未知数を文字でおこう

わからない問題に直面した時、多くの生徒たちはまず白紙です。ESCAの生徒たちはまずなんでもいいから書く（ほんとになんでもいいです。図形であれば条件を図形に書き写す、条件を表や図にしてみる、具体的な条件を決めて実験してみるなど）ということを徹底していますが、ただ単に条件を書き写すだけでは、そこで止まってしまいます。
実を言うと、未知数を文字でおくこと自体はそんなに難しいことではありません。しかし、数学に慣れないうちは意識をしないと意外とこの作業ができないものです。これはほとんど癖や習慣に近いものなので、感覚的に未知数を文字で置けるようになるまではしっかりと意識して問題に取り組む必要があります。基本的には、求めるものを文字でおくことが多いです。

 

2．他のものを表してみよう

ほとんどの生徒がつまずいているのがここの「他のものを文字で表す」という作業です。未知数を文字で表したはいいものの、そこで止まってしまう・・・。未知数を文字で表すだけではあまり意味がないことは、以下の図を見ていただければ納得いただけるかと思います。10という長さをある長さで切り分けました。その片方の長さをxと表します。しかし、これだけでは問題は解けません（もちろん解ける場合もありますが）。



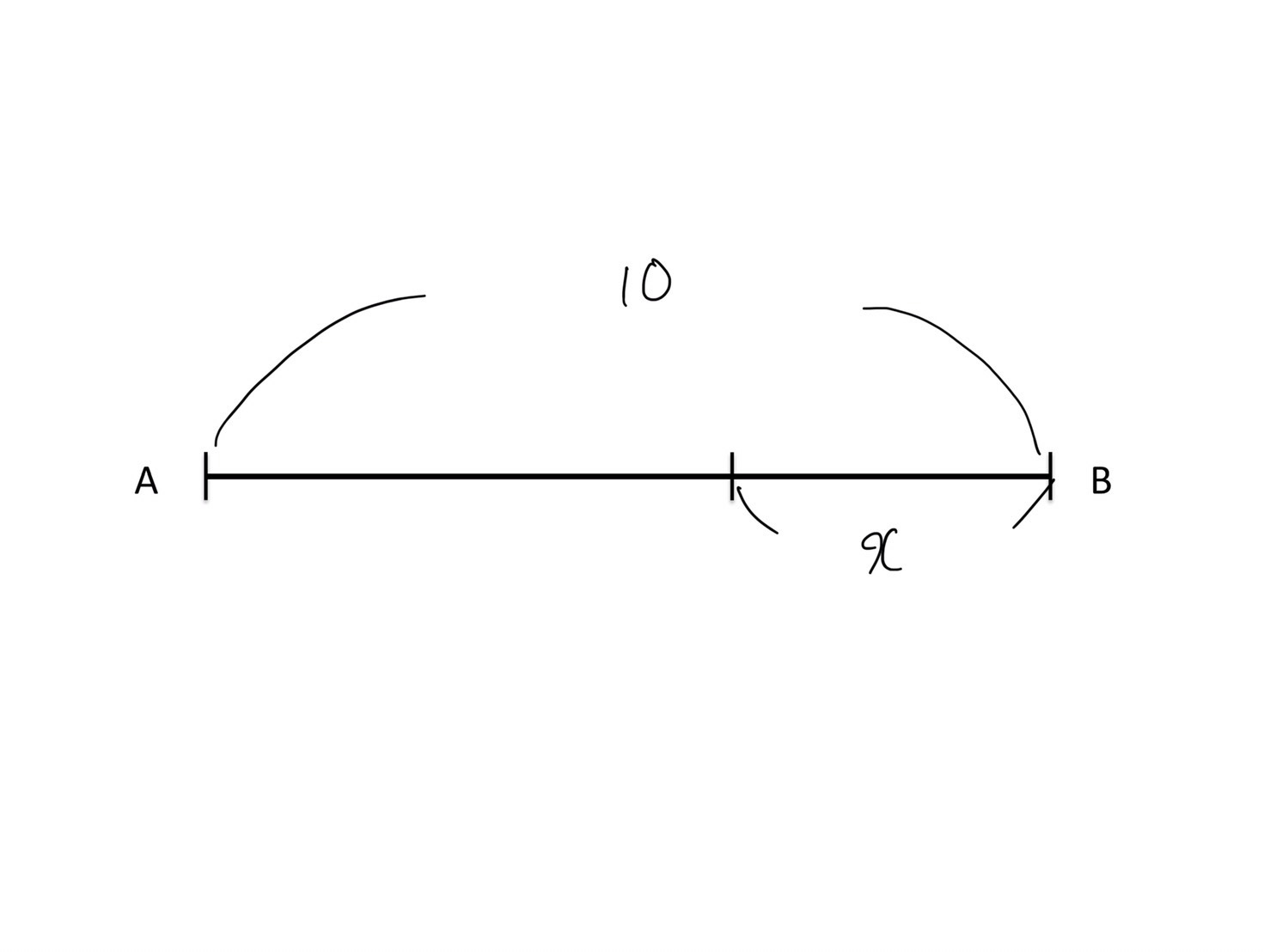
要するに、これだけでは一つの変量を一つの文字で表しただけで、その煩雑さは変わらないのです。しかし、もう片方の長さを10−xと表すことで、二つの量を表すことができます。片方の長さが変わると、もう一方の長さが変わる、つまり、二つの変量が存在するのですが、これをxという一つの変量で表すことができるわけです。今は二つの変量を一つの文字で表しただけですが、これがもっと多くの変量を一つの文字で表せるとしたらどうでしょう。随分扱いが単純になりますね。解法が初めから分かっていれば良いですが、解法やアプローチが思いつかない場合は、より多くの未知の量を文字で表し、その間にある関係式を考えることが有効です。

 

そして、以前ブログ「学習効率を上げるために書く回答」でも書いた通り、視覚的に捉えなければ何を文字で表せばよいかということは分かりにくいです。他のものを表すということを意識できても、表すものを見つけられなければ意味がありません。図形や、グラフ、問題の条件をまとめたメモなど、必ず視覚で問題を捉えることを忘れないでください。

 

3．表した量の関係式を考えてみよう

ここまでできればあとは式を作るだけです。不等式まで話すと長くなるので、今回は代表的な等式の作り方を紹介していきます。

①問題文の条件を利用する
これは一番簡単なパターンです。②と組み合わせることもありますが、たとえば、「AB=10となるとき」などは分かりやすいですね。ABの長さを文字で表してあげれば、その式をABの代わりにいれてあげるだけです。
「〜のとき」「〜となる」などが問題文に登場するときはこのパターンが多いです。これを使いこなすには「日本語から数式に訳す」という作業がひつようなこともありますが、これについては後日こちらのブログにて解説します。

②図形の性質を利用する
①と組み合わせたりします。正方形、平行四辺形、正三角形などの基本図形はもちろんですが、ベクトルの内積、関数（判別式を用いる解法や接線）などでも活躍します。
その図形が満たすべき性質を等式にします。例えば正方形であれば、隣り合う辺の長さを文字で表して等号で結ぶなどが有名です。図形の性質を覚えていなければもちろん解けないですが、ただ文字情報だけで性質を暗記していても等式に結びつきません。これらも必ず図を描いて確認するのが効果的です。

③公式を利用する
みなさんは公式というものをどのように捉えているでしょうか。数学に限らず物理でもそうですが、「答えを素早く導き出すもの」という捉え方をしている方がいらっしゃいます。その認識も間違ってはいないかもしれませんが、その認識だけで公式を捉えているのであれば、些かもったいないです。
各種公式は方程式を作る材料です。そもそも公式は、そのほとんどが等式であるがゆえに、代入するだけで方程式が完成します。しかも、公式の変数に値を代入する、公式の変数を文字で表すという作業を行うだけなので、「次に何を表せば（求めれば）良いか」が分かりやすいのです。

 

4．まとめ

数学がわからない時は闇雲に勉強してもうまくいきませんし、効率的ではありません。作文と同じで、まずは最初の一文を書くのに時間を使ってしまい、そのうち勉強をやめてしまう、ということになりかねません。今回記事にした「まずは未知数を文字で置いてみる」→「他のものを文字で表してみる」というプロセスは、まさに作文の「一文目を書く」という感覚に近いものです。まずはむやみに悩まずに、未知数を文字でおくということを考えてみてください。
未知数が置けない場合や、問題文で未知数が与えられている場合などはまた別のアプローチがあるので、後日紹介したいと思います。